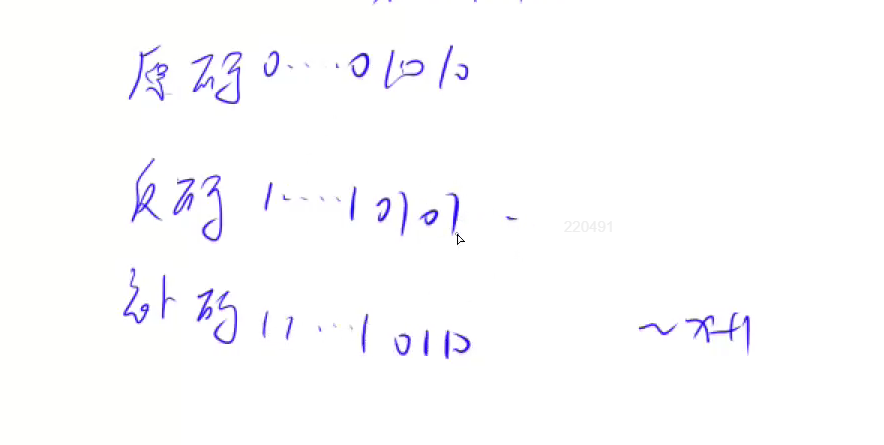基础算法

快速排序

思想

代码

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int x = q[(l + r) / 2], i = l - 1, j = r + 1;  // x 一般取中间 左右都行不过超时
    while(i < j)
    {
        while(q[++i] < x);
        while(q[--j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

归并排序

思想

代码

int q[N], tmp[N];

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int mid = r + l >> 1;

    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
        if(q[i] <= q[j]) tmp[k ++] = q[i ++];
        else tmp[k ++] = q[j ++];
    while(i <= mid) tmp[k ++] = q[i ++];
    while(j <= r) tmp[k ++] = q[j ++];

    for(i = l , j = 0; i <= r; i ++, j ++) q[i] = tmp[j];
}

二分

整数二分

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;  // 如果 l = r 下取整不变
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

浮点数二分

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

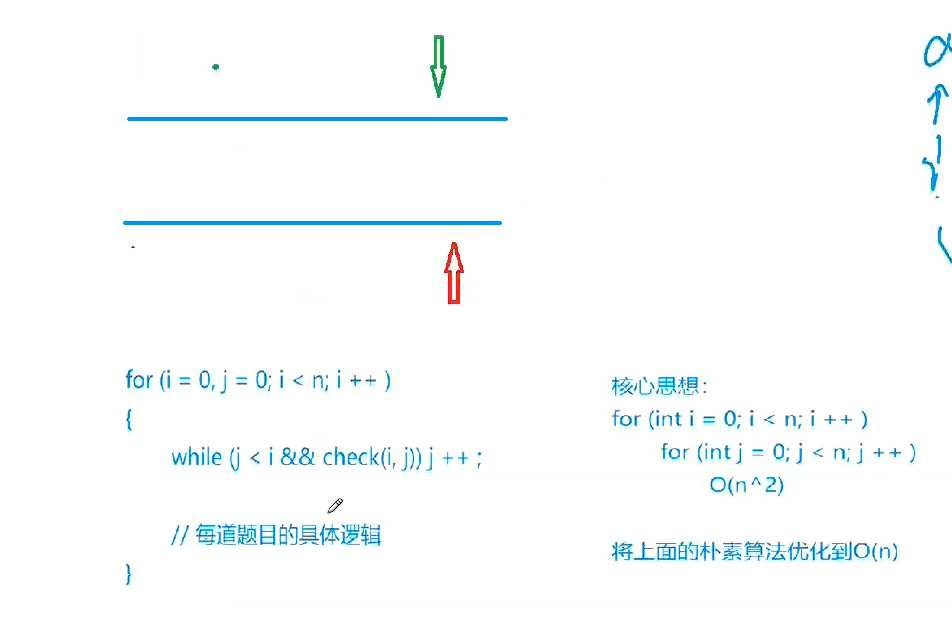
双指针

1.核心思想

位运算

原码，反码，补码

1.正数：原码反码补码相同

2.负数

对应的二进制原码：10000001
对应的二进制反码**（**符号位不变，其它位取反**）：11111110
对应的二进制补码**（**反码+1**）：11111111

3.运算：

10 的原码为 ：0 1010；

10 的反码为： 0 1010；

10 的补码为： 0 1010；

-13 的原码为：1 1101；

-13 的反码为：1 0010；

-13 的补码为：1 0011；

那么 10 - 13 = 01010 + 10011 = 11101（补码）

其反码为：11100；

其原码为：10011，十进制数为-3。

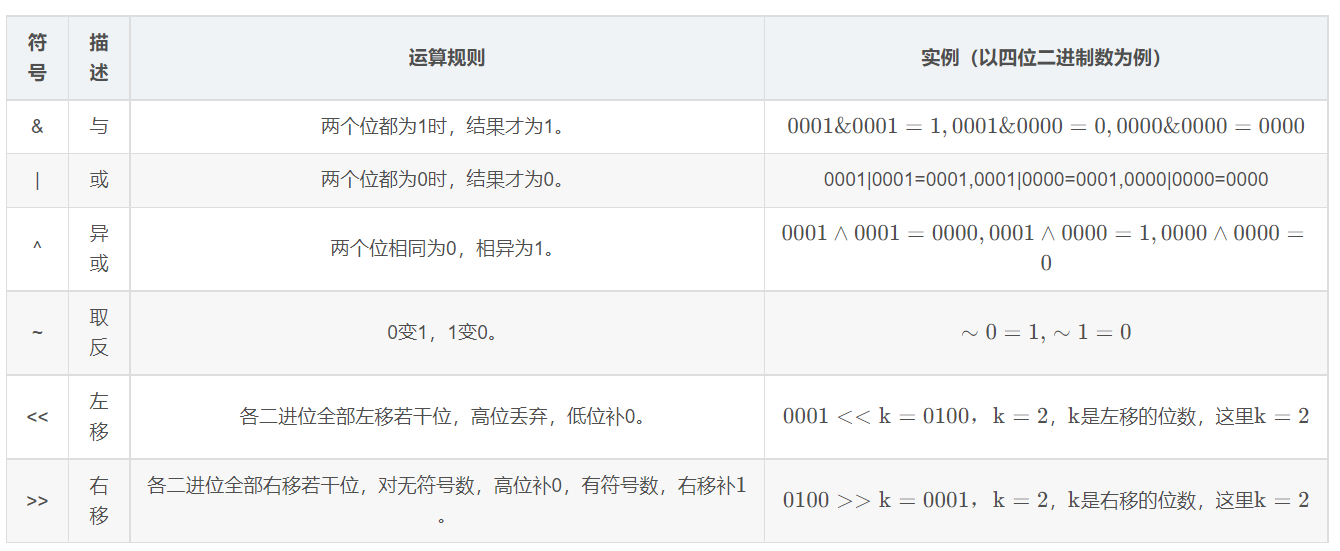
1.运算操作

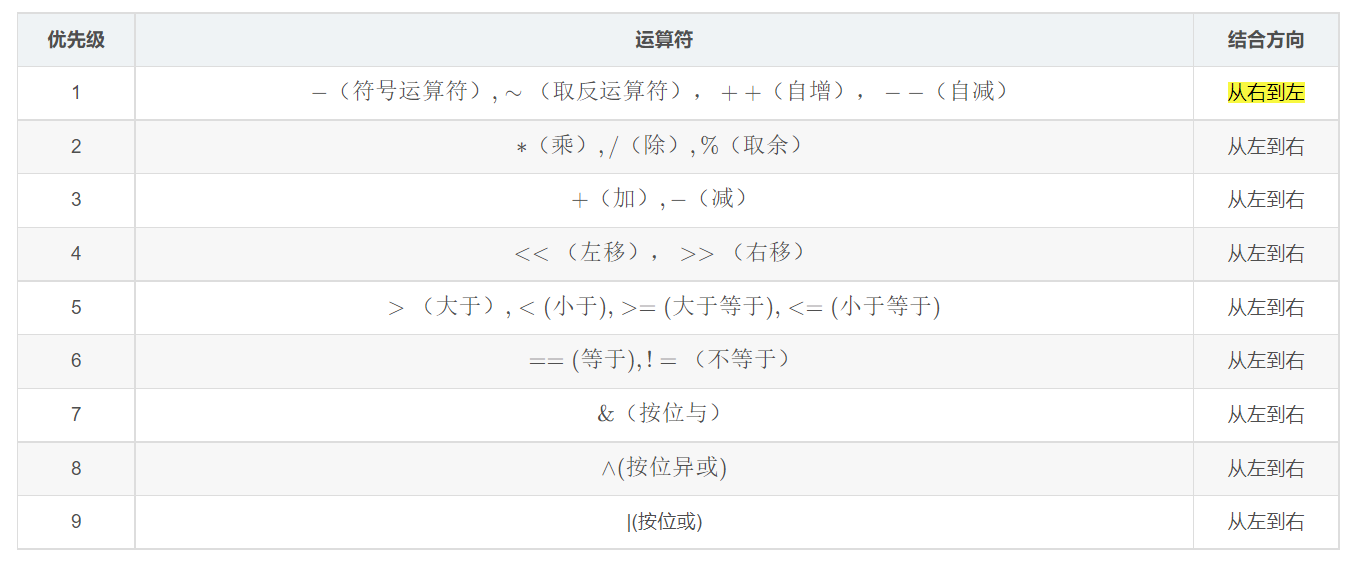
2.优先级

3.运算律

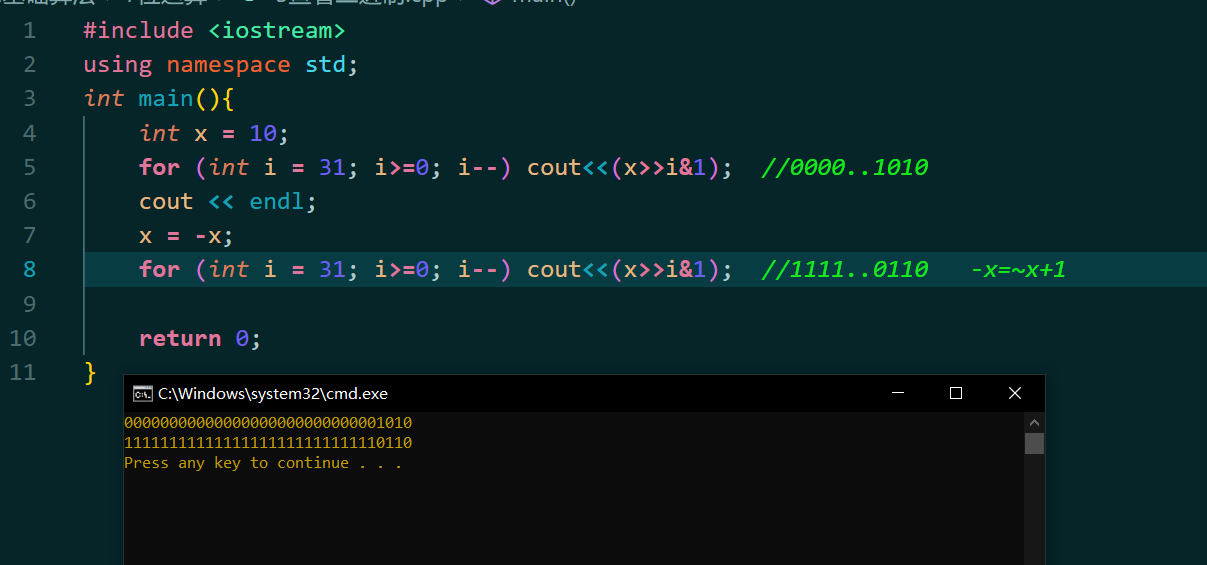
相关操作

查看二进制数

注：1.（-x）=(~x+1)

​ \2. x&-x= 10; (二进制)_

lowbit 操作

int lowbit_x(int x){
    return x &(-x);  // -x=(~x+1)
}

除法

将 x 左移一位实现 × 2 ，将 x xx 右移一位实现 ÷ 2

a < < 1 ≡ a ∗ 2 a

a > > 1 ≡ a / 2 a

交换整数

void swap(int &a,int &b){
     a ^= b;
     b ^= a;
     a ^= b;
 }

奇偶数

我们知道，在二进制中，最低位决定了是奇数还是偶数，所以我们可以提取出最低位的值，即与 1 相与即可实现目的，为 0 则是偶数，为 1 则是奇数。

绝对值

对于正数而言，补码就是原码，所以按位取反再+ 1 +1+1 则得到对应真值负数的补码，而对于负数，其补码进行按位取反再+ 1 +1+1 则得到对应真值正数的补码，变为原码。那么知道这个我们就可以特判是否为负数==（这里通过右移 31 3131 位，若为正数，则得到的是 0 00，若为负数，则得到的是 − 1 -1−1，而 0 00 的补码为 0000 00000000,− 1 -1−1 的补码为 1111 11111111，根据异或性质即可判断。）== 再进行反转即可实现求绝对值了。如下：

int abs(int a){
    return a ^ (a >> 31) ? a : ~ a + 1;
}

位运算实现对 p 取余（p 为 2^k)

int mod(int a,int p){
    return a & (p - 1);
}

例题

1.统计 1 的个数

​ 给定一个长度为 n 的数列，请你求出数列中每个数的二进制表示中 1 的个数。

#include <iostream>
using namespace std;
int lowbit(int x){
    return x & -x;
}
int main(){
    int n;
    cin >> n;
    while (n--){
        int x;
        cin >> x;

        int res = 0;
        while(x) x-=lowbit(x),res++;
        cout << res << ' ';
    }

    return 0;
}

思路： 1. x 与自身-x 求& 得到最后位 1 开始之后的值 如 10000100101000 得到 1000

2.x 减去 1000 就消去一个 1 直到 x 为 0

解法二：

int count(int x){
    int cnt = 0;
    while(x){
        x = x & (x - 1);  //消去后面1
        cnt ++;
    }
    return cnt;
}

2.O(1)时间检测 2 的幂次

首先我们知道 2^k 是大于 0 的，这里我们需要特判，同理，2^k

的二进制表示中只有 1 个 1，故我们可以利用 x & ( x − 1 )来消除唯一的 1 判断是否等于 0 00 即可。

class Solution {
public:
    bool checkPowerOf2(int n) {
        // write your code here
        return n > 0 && (n & (n - 1)) == 0;
        // return n > 0 && (n-=lowbit(n))==0；
    }
};

3.数组中奇数个数的数

1. 交换律：a ^ b ^ c <=> a ^ c ^ b
2. 任何数于 0 异或为任何数 0 ^ n => n
3. 相同的数异或为 0: n ^ n => 0

var a = [2,3,2,4,4]

2 ^ 3 ^ 2 ^ 4 ^ 4 等价于 2 ^ 2 ^ 4 ^ 4 ^ 3 => 0 ^ 0 ^3 => 3

for(auto c:nums)
      ret ^= c;

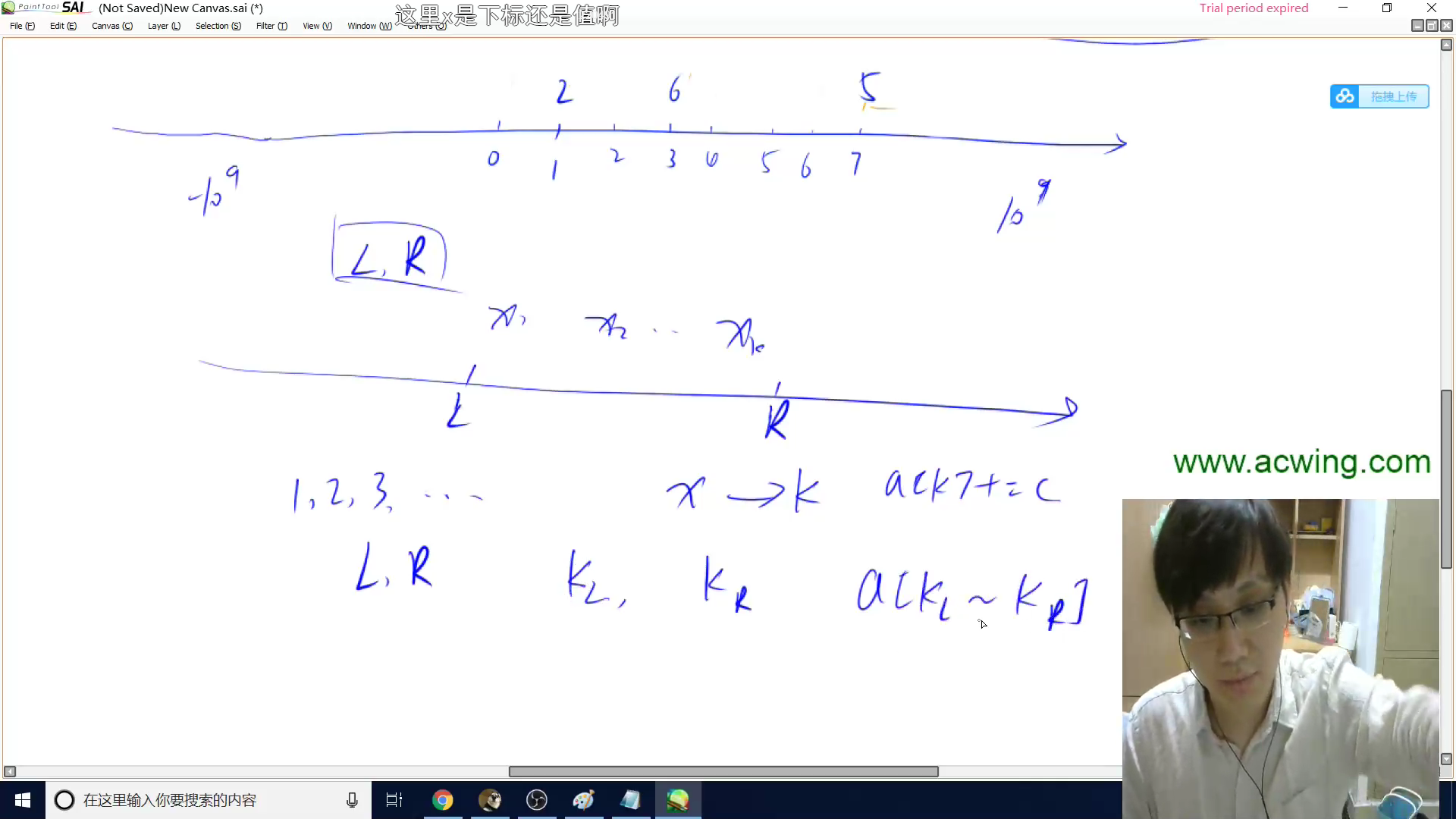
离散化

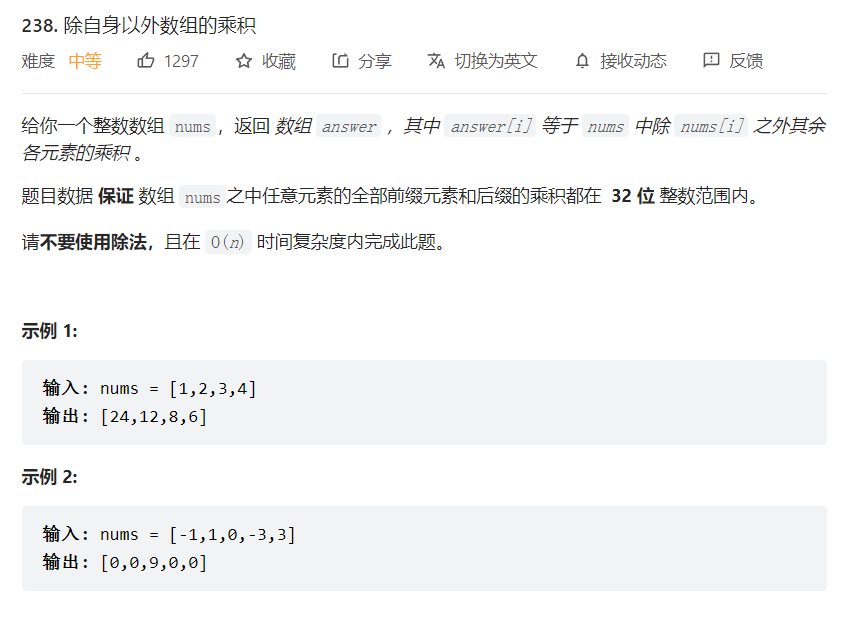
前缀和

1

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n=nums.size();
        vector <int> l(n,1),r(n,1);
        vector <int> res(n);
        for(int i = 0 ;i < n -1;i++)
            l[i+1] = nums[i] * l[i];
        for(int i = n - 1 ;i >= 1;i--)
            r[i-1] = nums[i] * r[i];
        for(int i =0; i<n;i++)
            res[i] = l[i] * r[i];
        return res;
    }
};

数组子串

class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
    unordered_map<int,int> mp;
    mp[0]=1;
    int res=0,pre=0;
    for(auto x : nums)
        {
            pre+=x;
            if(mp.count(pre - k)){
                res +=mp[pre - k];
            }
            mp[pre]++;
        }
    return res;
}
};

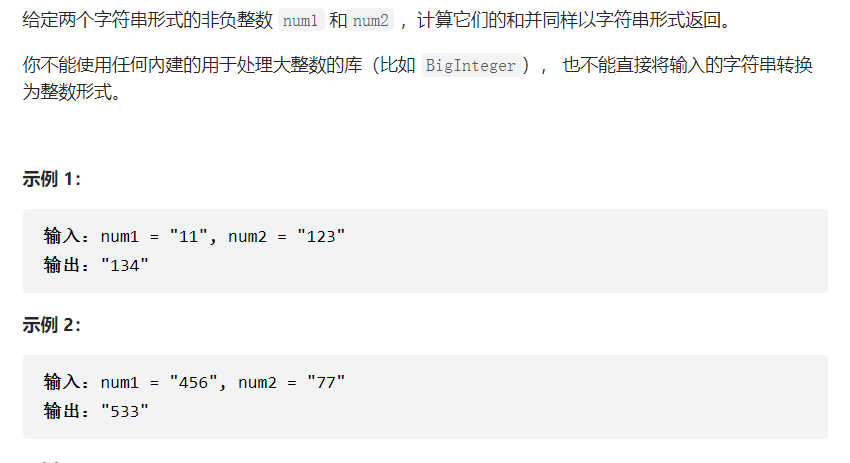
高精度

加法

string 版

string addStrings(string num1, string num2) {
        int i = num1.length() - 1,j = num2.length() - 1,add = 0;
        string res="";
        while(i >= 0 || j >=0 || add != 0)
        {
            int x = i >=0 ? num1[i] - '0' : 0;
            int y = j >=0 ? num2[j] - '0' : 0;
            int z = x + y + add;
            res.push_back('0' + z % 10);
            add = z / 10;
            i--;
            j--;
        }
        reverse(res.begin(), res.end());
        return res;
    }

vector 版

vector<int> add(vector <int>&A,vector <int> &B)
{
    vector<int> C;
    int t=0;  //进位
    for (int i = 0; i < A.size() || i < B.size(); i++)
    {
        if(i<A.size())  t+=A[i];
        if(i<B.size())  t+=B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if(t>0)  C.push_back(1);
    return C;
}
// 预处理
for (int i = a.size() -1; i>=0; i--)  A.push_back(a[i]-'0');
for (int i = b.size() -1; i>=0; i--)  B.push_back(b[i]-'0');

链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *head=nullptr, *tail=nullptr;
        int carry=0;
        while (l1||l2)
        {
            int n1 = l1 ? l1->val : 0;
            int n2 = l2 ? l2->val : 0;
            int sum=n1+n2+carry;
            if (!head)
            {
                head =tail= new ListNode(sum % 10);
            }
            else
            {
                tail->next = new ListNode(sum % 10);
                tail = tail->next;
            }
            carry = sum / 10;
            if(l1)
                l1=l1->next;
            if(l2)
                l2=l2->next;
        }
        if (carry>0)
        {
            tail->next= new ListNode(carry);
        }

        return head;
    }
};

乘法

vector<int> mul(vector <int>&A,int b)
{
    vector<int> C;
    int t = 0;
    for (int i = 0;i < A.size() || t; ++i)
    {
        if(i < A.size())  t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    while(C.size() > 1 && C.back() == 0)  C.pop_back();  //前导零
    return C;
}