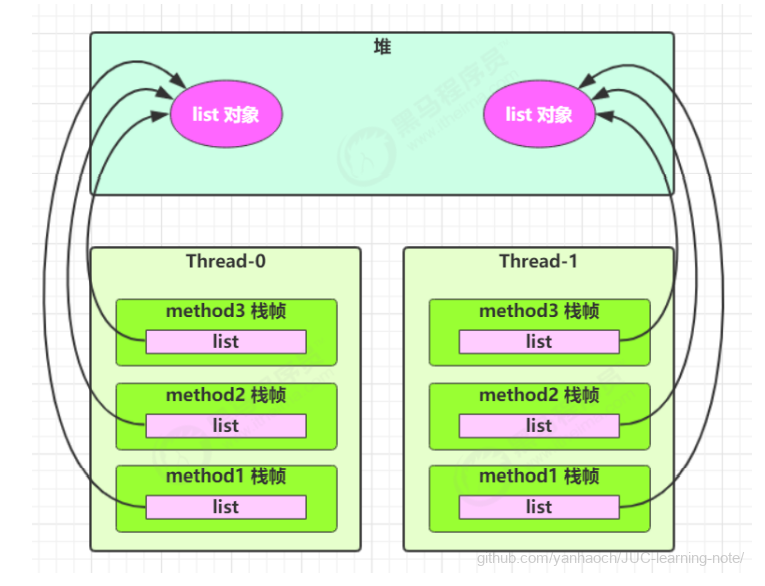
单链表

存储方式

  1. idx 表示结点编号

img

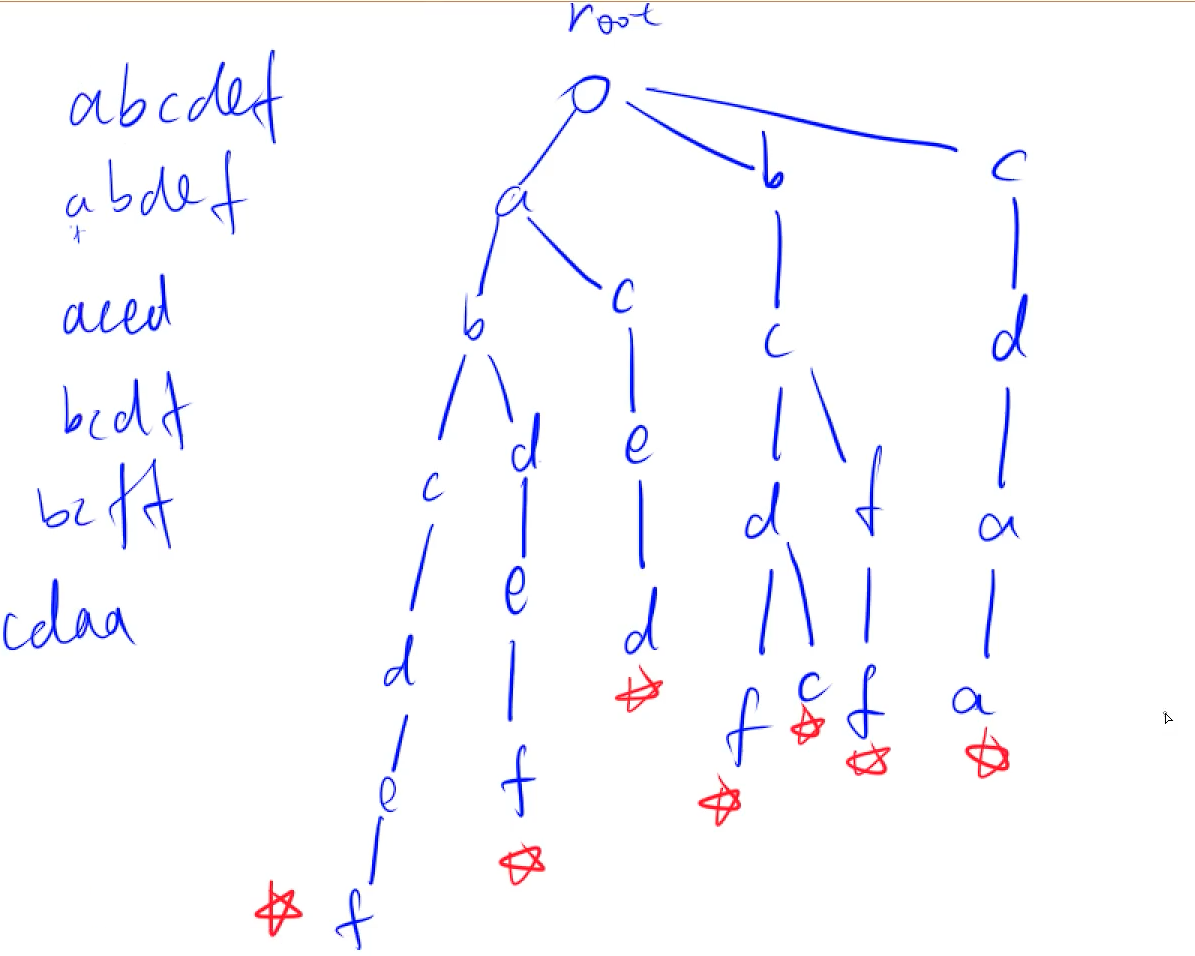
Trie

概念

img

  1. 存储

img

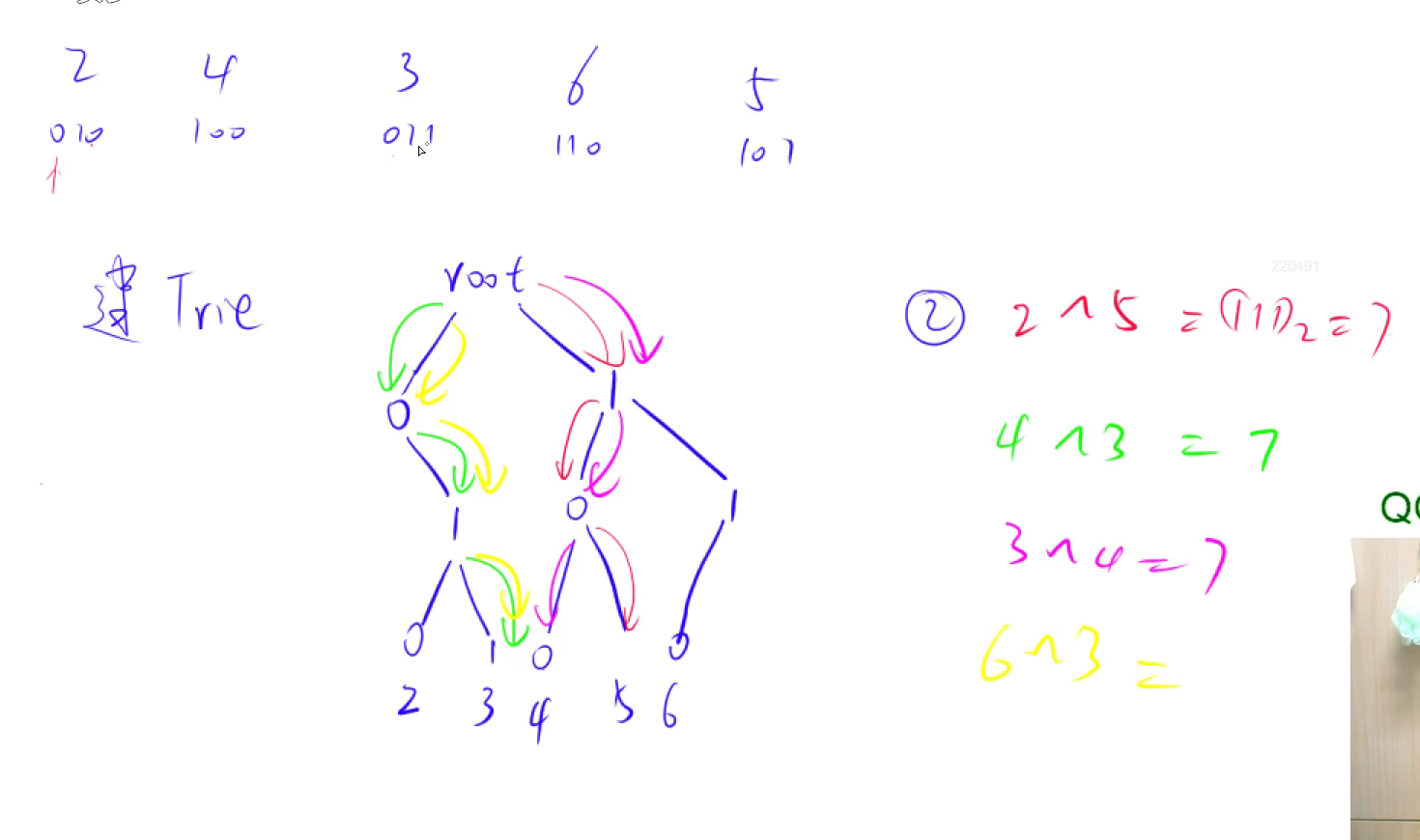
acwing143.最大异或对

img

思路：

1.将每个数放在树中

2.遍历一遍数据，从 31 位开始 是 1 找 0 是 0 找 1 没有则只能找当前相同 通过 res +=1<<i; 得到答案

img

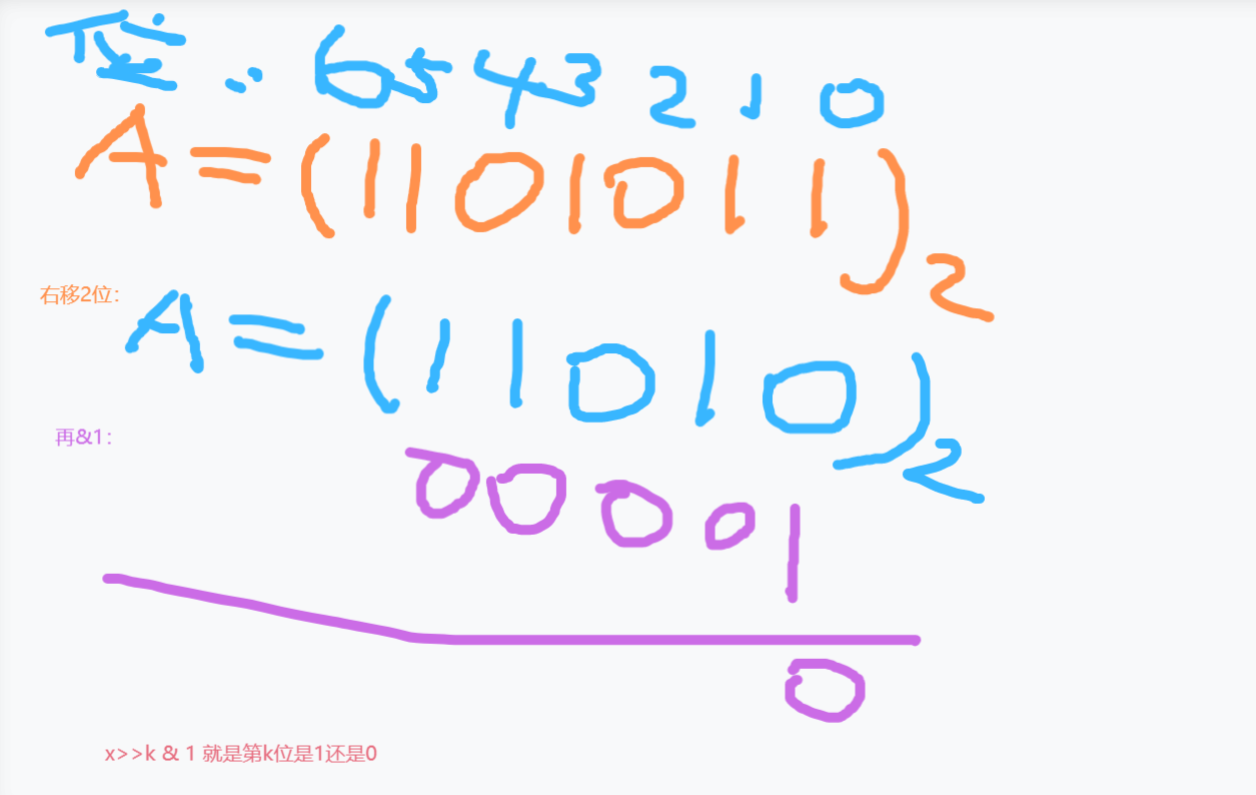
移位操作 预处理数据为二进制

x >> k & 1

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
using namespace std;
const int N = 100010, M = 3e7;
int son[M][2], idx;
int a[N];
int insert(int x){
    int p = 0;
    // ~i  i>=0的条件判断  -1 ->（11111111111111111111111）
    for (int i = 30; ~i; i--) {
        int &s = son[p][x >> i & 1];  //存在返回0  s为数组该节点左值引用
        if(!s) s= ++idx;
        p = s;
    }
}
int query(int x) {
    int p = 0, res = 0;
    for (int i = 30; ~i ; i--){
        int s = x >> i & 1;
        if(son[p][!s])  //核心算法  找异或不同为1
        {
            res += 1 << i;
            p=son[p][!s];
        }
        else
            p=son[p][s];
    }
    return res;
}

int main(){
    int n,res=0;
    cin >> n;
    for (int i = 0; i < n;i++){
        cin >> a[i];
        insert(a[i]);
    }
    for (int i = 0; i < n; i++) res=max(res,query(a[i]));
    cout << res;
    return 0;
}
  1. line9：>=0 可以用 ~i 表示
  2. line10，通过左值引用得到数组的值 对 s 修改便修改数组元素的值

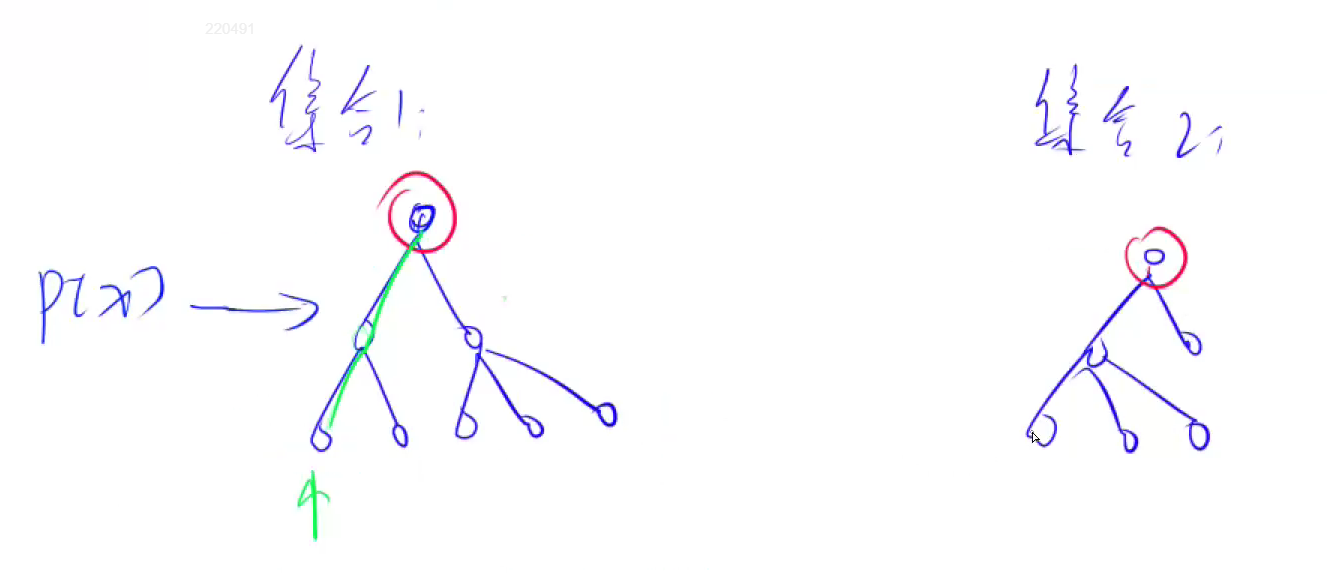
并查集

概念作用：

1.将两个集合合并 （近乎 O（1）复杂度）

2.询问两个元素是否在一个结合中

结构样图：

img

基本问题：

img

acwing836 集合合并：

题目

img

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
using namespace std;
const int N=100010;
int pre[N];
int n, m;
// int find(int x){
//     while(pre[x]!=x)
//         x=pre[x];
//     return x;
// }

// 路径压缩
int find(int x){
    if(find(x)!=pre[x])
        pre[x] = find(pre[x]);
    return pre[x];
}
int main(){
    cin>>n >> m;
    for (int i = 0; i <= n;i++) pre[i]=i;
    while(m--){
        char op[2];
        int a, b;
        cin >> op >> a >> b;
        if(op[0]=='M') pre[find(a)]==find(b);  // join函数
        if(op[0]=='Q'){
            if(find(a)==find(b))
                cout << "Yes" << endl;
            else
                cout << "No" << endl;
        }
    }
    return 0;
}

注：

1.数组 1~n 索引值 pre[i]=i i 是 n 个数 pre[i]表示自己的父亲

2.find 路径压缩 ：使一个集合中的父亲公共一个 近乎 O(1) 复杂度

acwing837 连通块中点的数量：

题目：

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int p[N], size1[N];
int n, m;
int find(int x){
    if(p[x] != x) x = p[x];
    return p[x];
}
// void merge(int a,int b) {
//     int x = find(a);
//     int y = find(b);
//     fa[x] = y;
//     size[y] += size[x];
// }
int main(){
    cin >> n >> m;
    for (int i= 1; i <= n;i++)
    {
        p[i]=i;
        size1[i]=1;  // 初始化size为1  只有祖先结点size才有意义
    }
    while(m--){
        char op[5];
        int a, b;
        cin >> op;
        // 1.连接a，b
        if(op[0]=='C')  {
            cin >> a >> b;
            if(find(a)==find(b))  continue;  //如果a，b在一个集合  则跳过
            size1[find(b)] += size1[find(a)];
            p[find(a)] = find(b);
        }
        // 2.判断a，b是否在一个集合(连通域)
        else if(op[1]=='1'){
            cin >> a >> b;
            if (find(a)==find(b))
                cout << "Yes" << endl;
            else
                cout << "No" << endl;
        }
        // 3.输出a所在集合的个数
        else{
            cin >> a;
            cout << size1[find(a)]<<endl;
        }
    }
    return 0;
}

注:

1.最后 3 查找该集合个数，以 size1 数组初始化每个集合个数为 1，

2.size1[find(b)] += size1[find(a)]; 把 a 插入到 b 下 b 的个数+=a 的个数

3.对应的：p[find(a)] = find(b); 把 a 插入到 b 下

食物链

题目：

思路：

img

哈希表

  1. 1e9 个数据 映射成 1e5
  2. 可能会引起冲突 通过一下两种方法解决

img

拉链法

  1. 开一个数组 1e5
  2. 若 11 23 映射到 3 ， 3 下开一个单链表

img

img

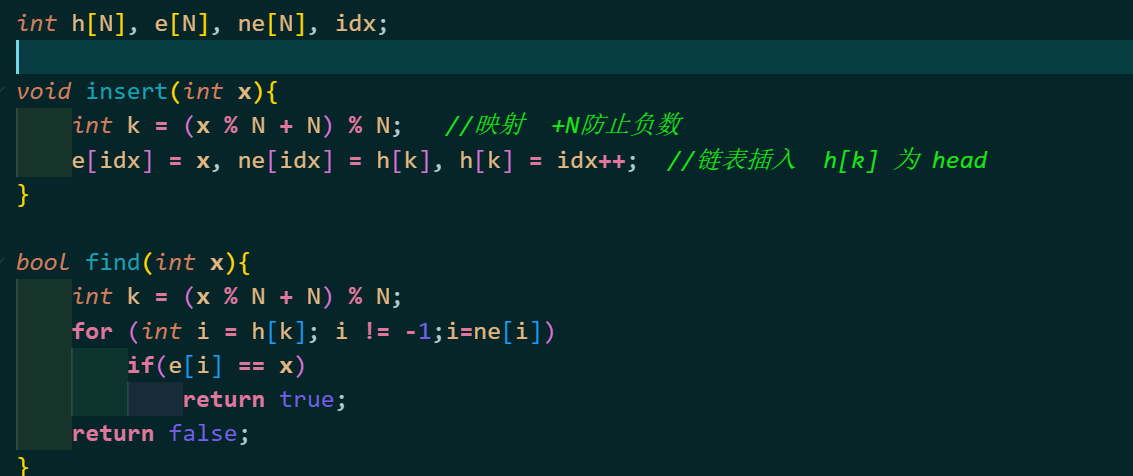
insert

1
2
3
4
void insert(int x){
    int k = (x % N + N) % N;   //映射  +N防止负数
    e[idx] = x, ne[idx] = h[k], h[k] = idx++;  //链表插入  h[k] 为 head
}

find

1
2
3
4
5
6
7
bool find(int x){
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1;i=ne[i])
        if(e[i] == x)
            return true;
    return false;
}

开放寻址法

1
2
3
4
5
6
7
8
9
10
11
12
13
const int N = 200003, null = 0x3f3f3f; //数组一般开两倍的第一个质数

int h[N];

// find函数 存在返回存的位置
int find(int x){
    int k = (x % N + N) % N;
    while (h[k] != null && h[k] != x){
        k++;
        if(k==N) k=0;
    }
    return k;
}

👀 字符串哈希

img

  1. 将字符串 前缀哈希值 1,2,3,4… 得到 1 - n 的哈希值
  2. 字符串转为 p 进制数
  3. 然后 mod 2^64 这里采用 unsigned ll 存储 溢出自动 mod
  4. 注： 不能映射成 0
  5. 经验规律： p =131 或 1333 1 Q= 2^64;
  6. 用 unsigned long long 存储 h，溢出相当于% Q;

求 L 到 R 的哈希值

img 1. 将 L -> 1 左移 扩大 至和 R 对齐

前缀哈希：h[i]=h[i-1]*p +str[i]

L-R 哈希公式： h[R] - h[L] * P^(R-L+1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;

typedef unsigned long long ULL;
const int N = 100010,P=131;
int n, m;
char str[N];
ULL h[N], p[N];  //p存放乘的次方

// L到R的哈希值
ULL get(int l,int r){
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main(){
    cin >> n >> m >> str + 1;
    p[0] = 1;
    for (int i = 1; i <= n;i++)
    {
        // 前缀哈希
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + str[i];
    }

    while(m--){
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if(get(l1,r1) == get(l2,r2))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}